[CHEMICAL ENGINEERING] Shortcut distillation - FENSKE-UNDERWOOD-GILLILAND-KIRKBRIDE! (how?) PART 3: Gilliland and Kirkbride Equation
In this post we shall continue the discussion of the Fenske-Underwood-Gilliland-Kirkbride method, in particular, the Gilliland and Kirkbride equations.
PART 3: GILLILAND-KIRKBRIDE EQUATIONS
So it has come to this! The final part of this three-part guide. The Gilliland equation is used to predict either the number of theoretical plates, or the theoretical reflux ratio, given the minimum number of plates as calculated by Fenske and the minimum reflux ratio as calculated by Underwood. The Kirkbride equation is a correlation used to determine the location of the feed plate (therefore, the number of rectification and stripping stages).
The Gilliland equation is defined as:
Yes, the equation looks... hairy. A common strategy to reduce the hairy-ness is to assign some dummy variables, like this:
- Determine what you want, exactly. Do you want to calculate for N, by adjusting R? Or do you want R, by adjusting N? For the sake of example, we want to calculate N, given R (we're still using the example).
- Calculate Ψ from the third equation.
- Calculate Ω from the first equation.
- Calculate N from Ω using the second equation.
- Calculate Ω from the second equation.
- Calculate Ψ from the first equation. This is really going to be ugly, so make sure you make a good Newton-Raphson assumption. Better graph the function and analyze it.
- Calculate R from Ψ using the third equation.
- NRECT is the number of rectification stages
- NSTRP is the number of stripping stages
- xF, HK is the heavy key component's feed concentration
- xF, LK is the light key component's feed concentration
- xB, LK is the light key component's bottoms concentration
- xD, HK is the heavy key component's distillate concentration
- B is the bottoms flowrate
- D is the distillate flowrate




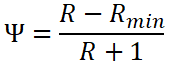




Comments
Post a Comment