The Fenske-Underwood-Gilliland-Kirkbride is a shortcut distillation method used to determine the number of theoretical plates for a distillation column. While the calculations resulting from this is barely accurate in real-life settings, the technique is normally used as a first estimation of how... high your tower would look like 😅
So we shall discuss it here, since my former students keep on asking me about this strategy for their plant designs (and I can't be bothered teaching it again and again, haha).
PART 1: FENSKE EQUATION
Anyway, as an example, let's assume that there is a debutanizer operating at 10 atm, separating 1000 kmol/hr of a saturated liquid feed with the following composition (in mol%):
I wanted to design the column such that 95% of n-butane is recovered at the distillate and 95% of i-pentane are recovered at the bottoms, respectively.
First, what I would do is to of course, take the vapor pressure (Antoine!) coefficients of each compound. Then, I would arrange them according to boiling points at 10 atm:
The Antoine coefficients are actually in terms of Kelvin (for temperature) and bar (for pressure), but any vapor pressure correlation should do.
Anyway, as it can be noticed on the table (and as expected obviously) n-butane and isopentane's boiling point readings are (I don't know what word should I use here, lol) 'right next to each other'. We can then assign n-butane as what we call the "light key" of the mixture, and isopentane as the "heavy key". For viewing purposes, we shall color the "light key" as yellow, and "heavy key" as blue.
The implication of doing so is as follows: as a rough approximation, we can say that the compounds above the "light key" should ideally go to the distillate, and that the compounds below the "heavy key" should ideally go to the bottoms. Therefore, we can say that propane and isobutane are "light non-key" compounds, and we can also say that n-pentane and n-hexane are "heavy non-key" compounds. This is important as it allows us to setup our first Fenske iteration.
While approaches may differ, this is what I usually do: I tabulate all the information based on molar flowrates and concentrations. Setting up for my first iteration:
What I did is:
Next. I'm supposed to do dew point calculations for the distillate and bubble point calculations for the bottoms (check your SVNA!) to determine the distillate temperature and bottoms temperature. I'm showing my final, converged calculations, by the way.
If curious, I used MS Excel Solver to have the temperature converge to the correct value (of course you can always keep guessing temperatures, but that would be so unwieldy). Then next is to evaluate the geometric relative volatility with respect to the heavy key. This is done by dividing the K-value of each compound in the particular stream with respect to the K-value of the heavy key. Why the heavy key, you ask? It will be apparent come the computation for the Underwood equations. Anyway, showing my solution:
As you can see, I determined the relative volatility α of each component at distillate and at the bottoms. As a reference, the α for propane at the distillate is 27.0684 / 3.739 = 7.2390, and α for n-pentane at the bottoms is 0.30037 / 0.37392 = 0.85083. The mean relative volatility is calculated using geometric mean methods (the multiply then square root thing).
The next step is to use the Fenske equation (in its default form) to compute for the minimum number of plates. The Fenske equation is:
The definition of the variables are:
Anyway, if my advice of tabulating everything has been followed then it would be easy to retrieve these quantities. Just for the record, the values are as follows:
We then solve for Nmin, the minimum number of plates required which is equivalent to 6.49.
The job is not yet done, however (and actually this is the rather lengthy part): Remember that we assumed that all the light non-keys go to the distillate, and that all the heavy non-keys go to the bottoms? Obviously that isn't true and of course we have to account for that! In other terms, the initial assumptions for DxDi and BxBi have to be corrected. So using the minimum number of plates we calculated, we back-compute the flowrates of each compound at the distillate. Then by arithmetic, we can compute for their bottoms flowrates. A convenient way of doing this is by transforming the Fenske equation to be solved in terms of DxDi:
We assign component j as isopentane. We then assign i as the component in question, thus changing the definitions to the following:
As an example, we set i as isobutane. In that case, the values become:
Using that modified formula gives DxD,isobutane = 173.4605955. Anyway, a summary of values are here:
Now that we have corrected the values of DxDi and BxBi, are we done? Of course not. Chemical engineering isn't easy 😂 since we have changed the flowrates, this means that the compositions of the distillate and the bottoms have changed. This also means that the dew and bubble temperatures have changed! (yay!)
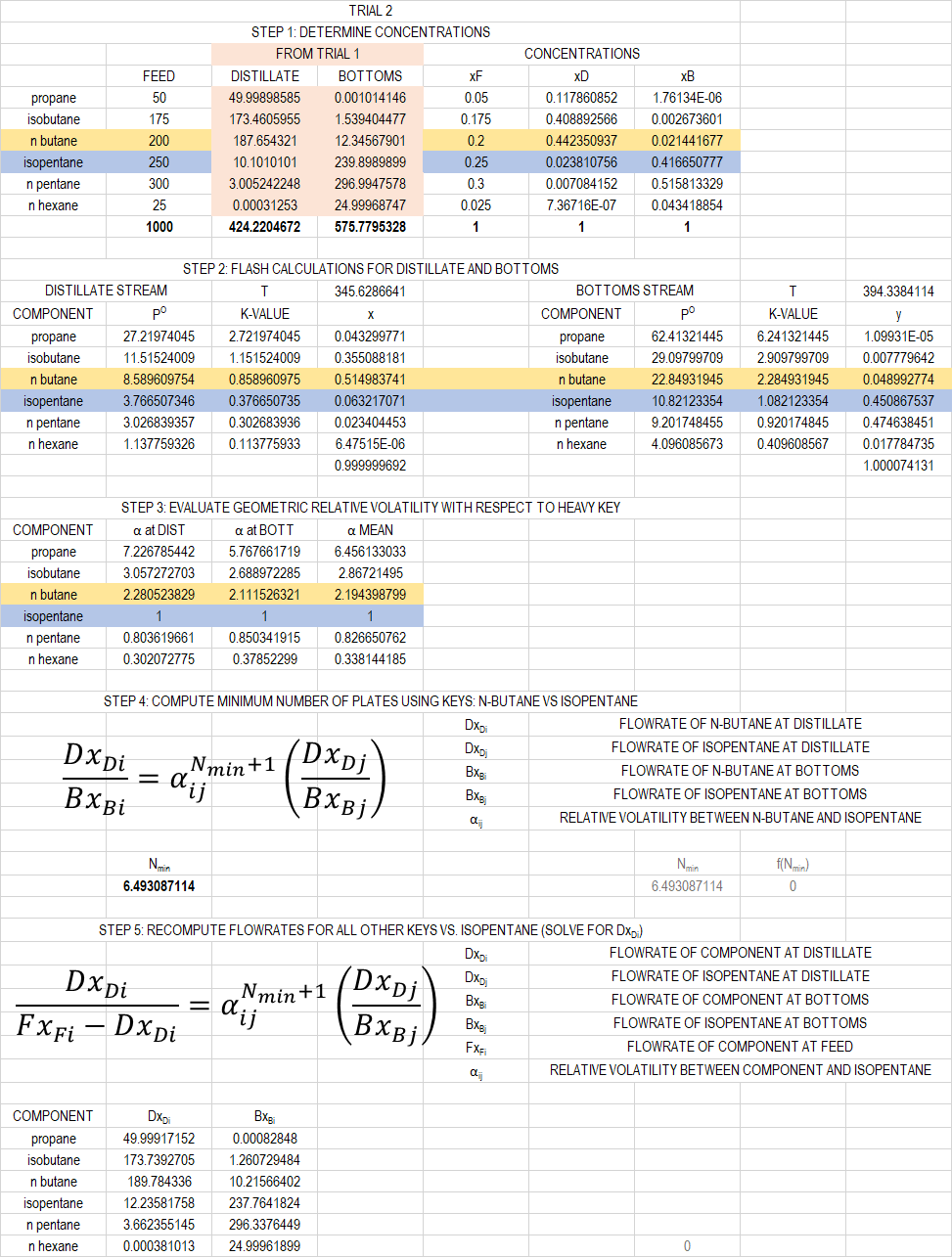
So what do we do? We re-compute the bubble and dew temperatures again! What I usually do is to replicate my original tabulations then change the flowrates as calculated previously. Then I can use Excel Solver again to have the temperatures converge again. As a guide, this is my trial 2:
As it can be seen, the minimum number of plates changed values, too. This iteration keeps on going until either:
Personally, I look at the temperatures. Anyway, after five iterations (this should actually be iterated more, but for the sake of brevity we just do five iterations), the result is:
So we need around 6.5 stages. In the next post we shall discuss the use of the Underwood equation to determine the minimum reflux ratio (and why the relative volatility calculations are based on the heavy key!)
Comments
Post a Comment